Science versus the “eye test” in selecting the college football playoff teams
Note: this paper will be published in Skeptic Magazine in March, 2017
In case you are not familiar with how college football determines the four teams that are picked to contend for the national championship, I refer you to the Selection Committee Protocol which is a guide on how the committee chooses the four playoff teams at the end of the regular season and after the league championship games. The first words of the protocol are telling: “Ranking football teams is an art, not a science.” The protocol specifically calls into question any rigorous mathematical approach: “Nuanced mathematical formulas ignore some teams who “deserve” to be selected.” For those that are not aficionados of the college football selection, the previous selection process used computer polls as one third of the formula to determine the final two teams (before the four-team process was initiated in 2014 – the other two thirds of the formula came from the Associated Press and Harris polls). What I hope to show in this essay is that 1) humans are primed with natural biases (whether they realize it or not) and therefore, are not effective at simultaneously considering the huge amounts of data available and 2) computer algorithms are spectacularly successful at analyzing massive data bases, sometimes called “deep data”, to ascertain the best choices for the playoff system.
So what are the guidelines that instruct the 13 member college playoff panel? They are somewhat obvious and include “conference championship wins, strength of schedule, head-to-head competition, comparative outcomes of common opponents, and other relevant factors such as key injuries that may have affected a team’s performance during the season or likely will affect its postseason performance.” I hasten to point out that strength of schedule can only be determined by “nuanced mathematical” rigor. The guidelines fall into two categories: facts (e.g., conference champions) and opinions (e.g., whether a key injury will impact team performance). My argument is to eliminate opinions and choose the final 4 teams in the most rational and unbiased fashion — that is, use computer algorithms. Exceptions to the computer rankings could be made by the committee when facts like conference championships play an important role. For example, if Notre Dame and Florida State University each had one loss at the end of the season but the computer rankings had Notre Dame above FSU, the committee might override the computer rankings and choose FSU over ND if FSU won the Atlantic Coast Conference championship (ND is not in a conference and therefore cannot win conference championships). Let me spend some time justifying my proposed selection process.
I have created a table below which shows the top 15 teams in the final polls of the 2015 season along with their won-loss records for reference purposes. The first two polls are the AP and Coaches polls and the final two are the Sagarin and Colley computer polls. Keeping in mind that the computer algorithms that determine the computer polls have no human intervention (the data on wins and score differentials are simply entered into the matrices), it is remarkable that the computer polls agree so closely with the human polls particularly within the top 5 teams (remember there are 128 teams in the NCAA Division I Football Bowl Subdivision – FBS in 2015). The details of the computer algorithms are discussed at the end of the essay.
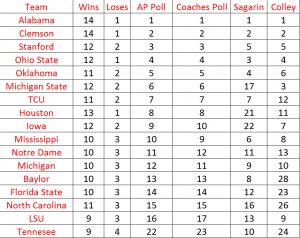Rankings from the final week of the 2015 season.
I agree that informed opinions can be important and a group of football experts might have insights into the game that mere mortals might not. Many of the committee members are former coaches and athletic directors, but I am concerned that opinions from former coaches and athletic directors might be tainted by the teams and conferences they come from (they might not even know they are biased). What is the difference between an informed and prejudiced opinion? I am not sure, but can these men and women be truly neutral? There is a massive amount of scientific research that shows that we have difficulties being unbiased. Nobel laureate Daniel Kahneman has written an entire book on heuristic and cognitive biases1. A good example comes from witnesses of crimes or traffic accidents. Any good detective knows to take eye-witness testimonies before the witnesses have had a chance to discuss the event because studies show that witnesses that share information will tend to foster similar errors about the event. And the research also shows that eye-witnesses are notoriously inaccurate. Elizabeth Loftus has written an immensely entertaining book about her research involving witness error and bias if you care to delve into the details2. Loftus writes: ” In my experiments, conducted with thousands of subjects over decades, I’ve molded people’s memories, prompting them to recall nonexistent broken glass and tape recorders; to think of a clean-shaven man as having a mustache, of straight hair as curly, of stop signs as yield signs, of hammers as screwdrivers; and to place something as large and conspicuous as a barn in a bucolic scene that contained no buildings at all. I’ve been able to implant false memories in people’s minds, making them believe in characters who never existed and events that never happened.” A recent study based on statistical analyses has shown that the writers’ and coaches’ college football polls are significantly affected by such things as point spreads and television coverage3.
If humans have all of these susceptibilities toward bias, why do we use humans to choose who plays in college football’s vaunted playoff system? Well, because humans are biased — they think they can choose better than nuanced mathematical formulas. But the nuanced mathematical formulas are completely unbiased — in other words, they use only raw game data usually related to wins/losses and score differentials. We can remove the most biased element in the system, humans, by relying specifically on science, logic, and mathematics rather than art or whatever else the committee protocol calls human intervention. It is absolutely archaic in the day of big data to ignore analytical models in favor of subjective comparisons. Do the coaches, atheletic directors, and politicians (e.g., Condoleezza Rice is on the committee but has virtually no “football experience” in her background) that make up the football committee understand the value of algorithms? I am not sure, but there is a wealth of research that says they should.
From my experience on football boards and chat rooms, nothing gets a fan’s dander up more than claiming computer models are unbiased. But they are. They start with only formulas melded together into computer algorithms. And the algorithms are based on sound mathematical principles and proofs. There are many college football algorithms used in computer ranking models and many of them are considered proprietary. More than 60 are compiled on www.mratings.com. The math can get pretty intense, but if you are interested in the details of the known algorithms, I recommend the book Who’s #1?: The Science of Rating and Ranking by Amy N. Langville at the College of Charleston and Carl Meyer at North Carolina State University4. The people that do these algorithms are steeped in mathematical prowess. For example, the Colley matrix was done by Wes Colley after he completed his PhD at Princeton University in astrophysics. Although the math can get tricky, the principle is rather simple. The algorithms typically involve matrices and vectors that simultaneously consider not only which team beat which opponents but which teams the opponents beat, and which teams those opponents beat out into n dimensions. In addition, difficulty of schedule and score differentials can also be incorporated into the algorithms. When we watch college football we get a sense of which team is best by comparing how each team plays against its opponents. But such opinions are hopelessly mired in the biases and are enhanced by the fact that preseason polls skew our perceptions before the season begins. The algorithms do precisely what human perception is trying to do but without any biases and simultaneously with a huge array of data 5.
I don’t understand the reluctance of the powers to be in college football to incorporate mathematical equations into the playoff system. These types of algorithms permeate the business community. Google’s PageRank ranks web pages using some of the same algorithms as computer models do to rank teams. Although it is a carefully guarded secret, Langville and Meyer 6 concluded, based on patent documents, that Google’s algorithm uses the Perron-Frobenius theorem which is also used by James Keener in his football rankings 7. The BellKor company won a Netflix prize of 1 million dollars for writing an algorithm that was 10% better than the one created by Netflix. Every time Netflix suggests a movie, it is exploiting the same kinds of algorithms used in football rankings. In fact, Langville and Meyer applied the algorithms behind the Colley and Massey methods to the Netflix movie ratings database and came up with a list of the top movies in their book (pages 25-27). No one complains about page ranks or movie suggestions being too nuanced in rigor. Can you imagine a committee trying to ascertain page ranks? No one promotes the “eye test” to rank web pages even though the eye test is commonly prescribed as the only legitimate way to determine which teams are the best in college football. Isn’t it obvious that this is about control rather than human abilities versus computer algorithms?
Deep data has been integrated into almost all sports. Witness the way professional baseball has dispensed with the traditional positions on the field in favor of moving players to positions where the hitter is most likely to hit. It is not unusual to see a shortstop in shallow center. The game was primarily changed when computers had the computing power to handle the large amounts of data that could be collected. Read Moneyball by David Lewis 8 to see how manager Billy Beane used statistics (now called sabermetrics) to take a struggling Oakland Atheletics team to the playoffs. Opinions of seasoned professional scouts that relied on the eye test to recruit talent have gone the way of the dodo bird.
In my opinion, nothing seems more egregious in the polls than the way teams are punished for losing when they play difficult schedules and other teams are favored for winning even with cupcake schedules. Let’s pretend we can determine the thirteen best teams in college football before the season and the number 13 team has scheduled all the top twelve teams during the regular season. The number 13 team could finish the season 0-12. The AP and Coaches polls would be extremely hard on the team and they would never rank the team in the top 25 even though we know by definition they are the 13th best team in the nation. But the computer algorithms would recognize the logic behind the difficult schedule and although they might not rank them 13th, they would probably have a good showing. The counter to this example is a team with a fluff schedule. The polls are notorious for ranking teams with perfect records higher than is sometimes justified when strength of schedule is considered. In theory, any team in the FBS could win all their games if they played lesser ranked opponents on their schedule. Fortunately it appears that the playoff selection committee has recognized that strength of schedule is an important factor and they do consider it. However, the committee’s willingness to consider head-to-head games seems logically misplaced. Let’s go back to our top 13 ranked teams again. If the number four team lost to the number 5 team and the number 5 team lost to the number 13 team, the committee would indubitably place the number 5 team into the playoffs over the number 4 team based on the silly head-to-head rule even though the computer algorithms would recognize the problem and consider the entire schedule of each team.
Although we don’t like to admit it, statistically improbable events can have a huge impact on single games which may never be noticed by the committee (or the computer algorithms for that matter – see the section on betting below). If anyone saw the national championship last year you could not be faulted for thinking that Clemson may have been the best team in the country even though they lost to Alabama (it hurts me to say this because I am an alumnus of Alabama and a huge Crimson Tide fan – I go way back to the Bear). Alabama had an onside kick that they recovered. It appeared to change the momentum of the game and yet, the probability of that onside kick being perfectly placed seems unlikely. Watch it for yourself below. Bama also needed a kickoff return and a few turnovers on their way to a 45-40 national championship victory. The point being that minutiae that would otherwise not have a big impact can and does play a role. It is the butterfly effect which teaches us that there is no right answer when it comes to rankings. The best we can do is create an unbiased mathematical system rooted in statistics and deep data with as little input as possible from naturally biased humans.
Last year I set out to test the college football computer algorithms by setting up a spreadsheet which monitored theoretical bets of $100 on each of the college games beginning on November 8 through the college bowl games. I waited until late in the season because, in theory, the algorithms work better with more data. I used Sagarin‘s predictor ranking which includes score differentials and home-team advantage. First a few words about these items. It is true that teams can run up the score although it rarely happens on a consistent basis. But most algorithms correct for large score differentials9 to avoid any advantages gained in the rankings from running up scores. Home-team advantage is an interesting subject in itself and is usually attributed to psychological effects of playing in a stadium full of the home-team fans. But these effects are difficult to test. The subject has also been addressed in the scientific literature, and much to my surprise, some studies show that referees can be influenced by the home crowd. For example, Harvard professor Ryan Boyko and his colleagues found that statistically referees favored the home team in 5,244 English Premier League soccer matches over the 1992 to 2006 seasons10. Regardless of the reasons for the effect of home-field advantage, algorithms can correct for it. Sagarin calculates a score to be added to the home team when betting.
The results of my theoretically betting are shown below for each week (the bowl season caused the number of games to vary in December). Had I bet $100 on each of the 287 games monitored I would have lost $700. So what’s so terrific about a ranking system that loses money in Vegas? It is simple – point spread. If Vegas lost money on college football games, there would be no betting. It is common for the media to give point spreads in games as a reflection of who Vegas thinks will win the game. But spreads are not about who is favored, the spreads are about enticing bettors to bet. With a point spread, Vegas does not have to predict winners, all they need to do is entice bettors by making the point spread seem to favor one side or the other. Vegas knows how to make money on all those built-in biases we have. They collect a fee (called a vig or juice) for handling the bet, and as long as they have about the same number of losers and winners, they take home a tidy profit. To make sure the winners and losers are equal, they shift the spread during the course of the week as the bets are placed assuring that the same amount of bettors are on both sides of the spread. Even the computer algorithms can’t beat the crafty Vegas’ bookies. Even though the computer algorithms are very good at predicting winners (near 60%), no algorithm (or, for that matter, any human) can beat spreads on a consistent basis11. But people keep trying.
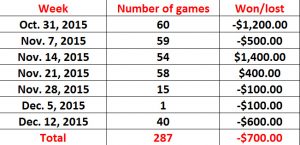Amount of money theoretically lost using Sagarin rankings.
Langville and Meyer point to two reasons why computer algorithms don’t beat point spreads; 1) The computer algorithms are created to predict rankings not score differentials. In the computations, they ignore important scoring factors such as strength of defensive backfields against high-octane passing attacks which might create lopsided scores even though the rankings rate both teams average. Then there are always the statistical flukes that occur in games as mentioned above which cannot be predicted. 2) Spreads are also difficult to predict particularly in football because points are tabulated in sets of usually 3, 6 or 7. Therefore, games tend to be multiples of these numbers rather than simple evenly distributed numbers.
I must conclude from the data that the only way to select the four teams that play at the end of the year in college football is to use computer algorithms. There should still be a committee that decides how to weigh such things as league championships. It will also be extremely important to make sure that the algorithms used are completely understood by the committee (no black-box proprietary claims). The algorithms need to be analyzed to determine which equations and factors give the most meaningful results and changed accordingly. Score differentials should be included within the algorithm after they have been corrected for the potential of teams running up the scores.
Appendix – a brief overview of linear algebra and rankings
There is no way in an essay I can do justice to the subject. But I did want to emphasize how these equations eliminate any bias or human influence. I highly recommend the Khan Academy if you want a brief overview of linear algebra.
Rather than use my own example, I have decided to use the data presented by Langville and Meyer because it is easier to understand when every team in the example has played every other team in the division. The data shown below comes from the 2005 Atlantic Coast Conference games.
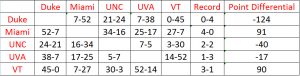The 2005 data from the Atlantic Coast Conference
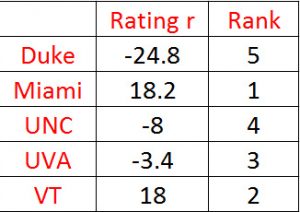
The Massey method of ranking teams was developed by Kenneth Massey for his honor’s thesis in mathematics while he was an undergraduate at Bluefield College in 1997. He is currently an assistant professor at Carson Newman University. Using his equations, the table above can be converted into a linear algebra equation of the form Mr = p where M is the matrix containing information about which teams played which other teams, r is the rating factor (which is equated to the ranking), and p is the sum of each team’s score differentials:
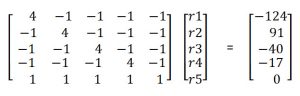
Note the diagonals of M are the games played and each -1 in the matrix shows that each team played every other team. The last row is a trick Massey used to force the ranks to sum to 0. The solution is calculated by inverting the matrix M and multiplying times p to obtain the following results 12:
- Kahneman, D. (2011) Thinking, Fast and Slow: Farrar, Straus and Giroux. ↩
- Loftus, E. and Ketcham, K. (1994) The Myth of Repressed Memories: False Memories and Allegations of Sexual Abuse: St. Martin’s Press ↩
- Paul, R. J., Weinbach, A. P., and Coate, P. (2007) Expectations and voting in the NCAA football polls: The wisdom of point spread markets: J. Sports Economics, 8, 412 ↩
- Langville, A.N. and Meyer, C. (2012) Who’s #1?: The Science of Rating and Ranking: Princeton University Press ↩
- I would like to thank Amy Langville for suggested changes here ↩
- see ref. 4 ↩
- Keener, J. (1993) The Perron-Frobenius theorem and the ranking of football teams: Society for Industrial and Applied Mathematics, 35, 80 ↩
- Lewis, D. (2003) Moneyball: W. W. Norton & Company ↩
- see ref. 4 ↩
- Boyko et al. (2007) Referee bias contributes to home advantage in English Premiership football: Journal of Sports Sciences, 25, 1185 ↩
- see ref. 4 ↩
- see ref. 4 for details ↩
As an avid consumer of football, both college and professional, I was always confused yet intrigued by the way rankings were set. I always thought it was a simple procedure by just looking at losses and wins and head to head match ups. Reading through this article made me realize how much more there is in the ranking of college football teams. I agree with the idea that rankings should be done with algorithms because this completely dictates out any sort of bias the human person is capable of. However, there still needs to be committees that oversee the process of ranking because although the algorithms aren’t flawed, there is factors like home field advantage, as mentioned in the article, that cannot be put into account when creating an algorithm. So far there is no “perfect” ranking system but it is about as close as it gets.
I thought it would be a fun and interesting read to see what goes on with the new college football playoff and what helps to determine who’s in and who’s out. Statistics are pretty tricky, and are not really an exact science. The rankings seem biased at times, the example in the essay put a number 4 team losing to a number 5 team, and that same number 5 team lost to the number 13 team. The committee could place the number 5 team in the playoff simply because they beat the number 4 team, ignoring the fact they lost to a not-top-ten team. Mathematical algorithms could possibly help in the selection, as long as strength of schedule is a factor. The Sagarin method tries to factor in home-field advantage and running up the score, which are important factors to think about. There is no real way to calculate home-field advantage other than looking at a team’s home record and making a judgment call, but it is implied to be a contributing factor to a team’s success on their own turf. Running up the score on a division opponent against a team at the bottom of the standings should not be a deciding factor on how a team is ranked, these (in my opinion) are obligatory exhibition games and a huge scoring margin could be a boost in confidence to the winning team. All said, algorithms could be implemented to help the college football playoff selection team pick who’s in and who’s not, rather than relying on an “eye-test” or bias.
This article argued for removing human choice in which teams are selected for the plays in NCAA College Football. It begins by describing the hopes of the article and explaining the guidelines that the current human committee uses to rank the teams. The article then discusses the exceptions for when humans should be used, such as conference games, but raises the point that no human can be completely unbiased even if they tired. They may hold biases based on which conference they came from without even being aware of that bias.The article then argues as to why computer based systems are completely unbiased, as they only follow mathematical guidelines. The article also points out the weak logic the committee would use based on head to head records to determine placing. An outliner is then brought up from the national championship game of 2016 where Alabama needed a series of spectacular plays to win despite the other team’s apparent superiority. The article then points out that spreads used in casino are to entice betters to bet; they are not used to predict a match’s outcome. The article concludes that computer systems are the only unbiased way to select the top four teams.
I enjoyed reading the article as it made me question why humans were still a part of this process. The study where Elizabeth Loftus adjusted peoples memories was very interesting. How often a football team appears on ESPN may not only change the average viewer’s opinion on who deserves to be in the top four, but the committee members as well. They may remember hearing so many positive things of a team, or so many negative things of a team, and those things will interfere with who the committee member picks to be in the top 4. A computer system would simply compare math, neglect any chance of a bias. This article also makes me wonder where else human bias could be replaced with mathematics.
The article was about the college football playoff system and how the use of people over computers is a mistake because of the bias involved when selecting the top four teams. There are many examples of what different kind of algorithms could be used to determine which teams are truly performing well rather than relying on the “eye test”. There is also a section about the types of algorithms, the practicality, and success of using them, not only in football, but in the business world as well (the example used in the article was Netflix). Later in the article, he discusses about betting on various teams and the success rate while using computers and linear algebra and how it still remains difficult to be successful because of the point system and the different variables involved in every game that are difficult to calculate such as having a good secondary defending a solid spread attack. Ultimately, the article points out the selection committee using the “eye test” would statistically be beaten by computers and algorithms each year and over the long run when it comes to unbiasedly choosing the top four teams in college football to enter the playoff.
This article was very interesting to me because I watch college football every year and I can never distinctly determine which four teams should be in the playoffs solely based on watching each team play or how strong each schedule is without being bias. I agree with what your ideas were and what the research you provided shows for the way the teams should be selected which was to use computers, linear algebra, algorithms, and real time statistics in order to select all four teams. I didn’t realize how practical, vital, and similar algorithms were till the example for that Netflix giving the prize of one million dollars to the person who created it because it was 10% better. It is probably a good thing that the algorithms don’t help on the betting in vegas or else it would be exploited or it wouldn’t exist. It makes sense though because there are a lot of variables in football that aren’t accounted for on a game to game basis and football scoring does have an odd scoring system. All in all I really enjoyed reading the article and I’ll try to pay attention to the progress of the methods the selection committee uses in the future.
With March Madness around the corner, I thought it would be a fun and interesting read to see what goes on with the new college football playoff and what helps to determine who’s in and who’s out. Statistics are pretty tricky, and are not really an exact science. Wins and losses have something to do about the selection, however how many division I schools end the season with the same record? How does strength of schedule come in to play, if at all? The rankings seem biased at times, the example in the essay put a number 4 team losing to a number 5 team, and that same number 5 team lost to the number 13 team. The committee could place the number 5 team in the playoff simply because they beat the number 4 team, ignorning the fact they lost to a not-top-ten team. Mathematical algorithms could possibly help in the selection, as long as strength of schedule is a factor. The Sagarin method tries to factor in home-field advantage and running up the score, which are important factors to think about. There is no real way to calculate home-field advantage other than looking at a team’s home record and making a judgment call, but it is implied to be a contributing factor to a team’s success on their own turf. Running up the score on a division opponent against a team at the bottom of the standings should not be a deciding factor on how a team is ranked, these (in my opinion) are obligatory exhibition games and a huge scoring margin could be a boost in confidence to the winning team. All said, algorithms could be implemented to help the college football playoff selection team pick who’s in and who’s not, but in the end I think there are too many things to factor in that can’t be quantified into data and simply plugged into equations.
This article reflects how Marc Defant wants to change the way the college football playoff process is used. The current process being used is a mixture of many facts and also a mixture of many opinions. Removing opinions towards determining the final four is very important and must be done. There can be many bias from past coaches and athletic directors when the committee is selecting. So despite all that Marc Defant believes in a different and more effective selection process for the final four which is based off only mathematical algorithms. Which will ensure the result in being more fair and less biased. As Marc Defant informs us that there is no true perfect way of deciding the final four, he believes that this method is the only way to get rid of the bias. Marc Defant explains in his introduction paragraph that algorithms can fix things like home team advantage, head to head competition, strength of schedule, etc. Concludingly, Marc Defant believes in using a formula developed by Kenneth Massey. He briefly explains Kenneth Massey’s formula in the passage, “Using his equations, the table above can be converted into a linear algebra equation of the form Mr = p where M is the matrix containing information about which teams played which other teams, r is the rating factor (which is equated to the ranking), and p is the sum of each team’s score differentials. But, still Marc Defant believes that the committee should still be there during the selection process but also know and understand the algorithm itself. So that now no bias or opinions could impact the decision being made and it comes down completely to the computer algorithm.
The amazing thing about sports is definitely how and whom create the rankings and determine the rating scales as indicated in this article towards college football. There is no perfect ranking system because the biggest problem with all is biases. If there were any injuries? If it was home field advantage? How the referees make calls determining which team is at a home game? and much more. Due to all these biases this can greatly curve the proper rating scale made by any human and even calculated by computer algorithms. Though proven time and time again computer algorithms always prove human minds wrong in any basis of logic. Though, the thing to consider is that computers can’t see everything the human mind can and can’t think the same way a human mind could. It will just never be possible. Though, I do believe that if we had computers solve out the problem on who will be ranked we will end up with the most fair outcome. Though, always there must be some type of human interaction with the rankings because it will give better playoff outputs for collge football rather than technology outputs because we have emotion. That is the whole problem with human biases because of emotion. Not saying all biases is bad but most are good in a certain setting like college football and determining the playoffs with the biases makes it all much so entertaining.
I love the topic you choose to write about. Other than being a HUGEEEE Bull fan, I have followed the Oregon Ducks for the last 5 years. I never really understood how the college ranking system worked. What I knew prior to reading article is that the rankings had something to do with Wins and Losses. But the Massey Method was something that I haven’t never heard of before. Although this is very interesting, I do not believe that you should not be able to use this equation to determine the rank. I feel that you cannot determine how a great a team is doing based on how many points they score over another team. Next, based on your study between computer algorithms I didn’t expect you to turn a profit on this test. When it comes to a lot of things I feel as though computer; better than that, technology is making a significant change on our human existence. This form of augmentation has created new opportunities of advancements for us all in some type of way. Being an Accountant, I am not sure how my day to day operations would be if I didn’t have my computer to compare forecasts. But, my computer cannot tell me what to make of what was projected. So, I do believe that computers are typically more reliable than humans in processing data. But in the end, the best decision are made by humans.
Essentially, Marc Defant hopes to eliminate the current NCAA playoff selection process which uses a combination of facts and opinions. Specifically, the elimination of opinions is extremely necessary when determining the final four. Bias from previous coaches and athletic directors may be present in the selection process and it can ultimately be unfair to teams with a great seasons. As such, Defant offers another selection process which uses only mathematical algorithms to eliminate bias. Even though he admits that there is no right answer to college rankings, eliminating bias gets us much closer to being realistic. He notes that, algorithms can correct things like home team advantage, difficulty of schedule, and score differentials for issues like running up the score. Ultimately, using a formula like the one developed by Kenneth Massey should be used. However, Defant states that the committee should still exist but have clear understandings of algorithms used. This way, a unanimous decision can be reached and the committee can focus on league championships.
I’ve never truly understood what made a team better than another in rank. Even in my high school days as a baseball player I saw the subjective ranking system that existed. Many times we would have a better record than most teams but be ranked lower because of our schedule. Objectively, we could never play against the “best” teams in the county and our season was essentially swept under a rug. Much is the same with college football. Bias is clearly something that has a lot of influence on these ranking systems and honestly, I think it’s good and bad. It’s good in a sense that we get to see the games that we all want to see. What I mean by this is that rivalries and games that draw a lot of emotion from the fans appear more often. However, this ranking system is bad because objectively, we never get to see the “best” teams square up against each other. Personally, I could go on a whole rant about how everything boils down to money and this is where the main bias may lie. It’s no coincidence that the teams with the highest paid coaches tend to have more championships. Without pushing further, if we lived in a perfect world where we actually cared about seeing the best teams play each other, there’s no doubt that we would have to use computer based ranking systems instead of our subjective system. Numbers simply don’t lie. However, I think we can all agree that numbers are boring compared to a fierce rivalry.
I’ve never truly understood what made a team better than another in rank. Even in my high school days as a baseball player I saw the subjective ranking system that existed. Many times we would have a better record than most teams but be ranked lower because of our schedule. As a result, we could never play against the “best” teams in the county and our season was essentially swept under a rug. Much is the same with college football. Bias is clearly something that has a lot of influence on these ranking systems and honestly, I think it’s good and bad. It’s good in a sense that we get to see the games that we all want to see. What I mean by this is that rivalries and games that draw a lot of emotion from the fans appear more often. However, this ranking system is bad because we never get to see the “best” teams square up against each other. Personally, I could go on a whole rant about how everything boils down to money and this is where the main bias may lie. It’s no coincidence that the teams with the highest paid coaches tend to have more championships. Without pushing further, if we lived in a perfect world where we actually cared about seeing the best teams play each other, there’s no doubt that we would have to use computer based ranking systems. Numbers simply don’t lie. I think we can all agree that numbers are boring compared to a fierce rivalry.
The whole college football ranking system is something that has forever confused me. Personally I have never been a fan of college football, it is not the sport that I do not like, but simply the ranking system. I am a huge NFL fan, a Buccaneer fan at that, I like the system it has. Al Pacino had it right when he quoted the novel “On Any Given Sunday”, I like this about the NFL because it does not matter what the eye test has to say, it is simply two teams going out on the field and playing for a winner, however this is about college and there is a ranking system that confuses me.
I like the computer and science behind the ranking system, well I do not like it per say, but I believe it to be a better system than the eye-test which is extremely biased. The science is better in my opinion because it uses integrated formulas digging into deep data, that humans can not break down as effectively. Some human play is still needed though, since the formulas do not take into account how hard the season match ups can be for teams, but this is something I would want to be eliminated. I believe that all human interaction for choosing the top four teams to play in the playoffs should be left for the computers. The eye-test brings into account how badly a team beat another team, or it looks at the coaches and they factor into it. It should be all about football and who is actually the best teams for the championship playoffs.
It is definitely very interesting to see how the rating systems in sports are made and who makes them and what factors rank the teams in any sport, but especially here in college football. Not every system that we use is perfect to be able to rank these teams, but the system that we use today definitely needs to be fixed with all the bias that is going around these days. Will there always be bias in our ranking systems? I think so, I think there has to be in sports. But with new research, it seems as if we can take all of that out and perfect our system, but I don’t think people are ready to take out the human factor in it yet. However, technology over time has proven the human mind wrong. When given the same task as a human, the technology always wins these days, and there is no bias in it. When this happens, everything in sports will be fair game to compete for spots in playoffs or etc. Personally I do not think that we need to take the humans out of the process completely but we need to let the computer come up with a selection of teams and then maybe let the humans make a decision from there because there are different conferences, different factors that I think the computer can’t see that the human eye or mind can.
I find it fascinating how controversial things such as the college football rating system tend to be; not because I’m surprised that people have their biases or that they can often care more about college football than who’s going to be our next president, but because we haven’t fixed the issue with the current system yet. Relatively everyone can recognize that the current rating system is imperfect. However, we have countless alternatives that can be used to perfect them system, all backed by research to prove their effectiveness, yet we’re still hesitant to take out the human factor in the rating system.
We live in a world surrounded by big data, statistics, and mathematical algorithms. If you go through an entire day and think about each and every thing that you come across, it’s all been broken down to a science, statistically analyzed and perfected to the best of our ability. A few examples would be, traffic lights, inventory programs for grocery stores and as mentioned in the article, web page ranking. You don’t see a person standing at the middle of every intersection directing traffic, nor do you see employees making a physical inventory count every single day to figure out what to order, just as we don’t have a team of individuals ranking web pages by hand. These systems have been improved by taking humans out of the equation and passing the job onto technology and the statistical and mathematical formulas that run throughout it, and yet, no one is complaining that these processes would work better by plugging humans back into the formula.
As humans, there are many things that are out of our control, including the ability to remain unbiased at all times. No matter how much the committee would like to convince everyone that they are unbiased while selecting the playoff teams, it’s simply out of their control. The human mind is an amazing thing, but it has been proven time and time again that it can be easily manipulated into thinking or feeling a certain way. This isn’t the case with using a statistical formula. The extent of the human-element in these formulas is data entry, leaving no room for biases, and that’s the way the playoff selections should be.
Time after time, technology has proven to be better than a human when given the same task. Technology is faster, more accurate, less prone to mistakes and above all else, unbiased. The sooner the NCAA can realize this and let up on their need to control everything going on, the sooner this game and the playoff selection process will become closer to being fair. While I do believe that the playoff selections need to be left to the many proven statistical formulas that can by employed, I also believe, as mentioned in the article, that there is still a need for human-interaction in the process when it comes to things such as weighing particular factors and analyze the results for accuracy.